01.2 Fonctions NON - ET (NAND) , NON - OU (NOR)
I. Relations en Algèbre Logique
L'algèbre obéit à certaines règles qui sont caractéristiques du système binaire. La connaissance des relations nous permettra, parfois, de simplifier les équations logiques.
1.1 Commutativité
Le produit logique (fonction ET) est commutatif ; on peut écrire :
De même, on peut commuter les termes d'une somme logique sans rien changer à l'expression :
1.2 Associativité
Les propriétés d'associativité sont applicables aux expressions logiques.
1.3 Distributivité
a) Distributivité de la fonction ET par rapport à la fonction OU.
On peut écrire : a ( b + c ) = ( a . b ) + ( a . c )
b) Distributivité de la fonction OU par rapport à la fonction ET.
On peut aussi écrire : a + ( b . c ) = ( a + b ) . ( a + c )
Conclusion : Les propriétés de l'algèbre logique sont les mêmes que celles de l'algèbre avec , en plus, la distributivité de l'addition logique (OU) par rapport à la multiplication logique (ET)
II. Relations Particulières
Elles permettent de simplifier des expressions logiques lorsqu'elles se présentent sous la forme des équations du tableau ci-dessous.
Équation |
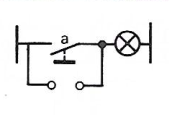
Représentation électrique |
Équation |
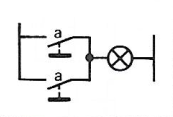
Représentation électrique |
a + 0 = a |
a + a = a |
||
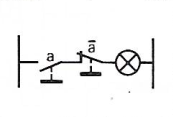
a . 0 = 0 |
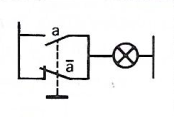
a . a = a |
||
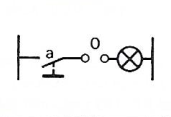
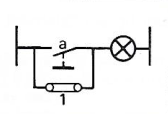
a + 1 = 1 |
|||
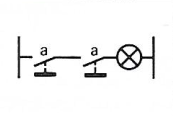
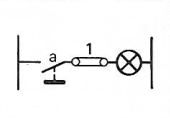
a . 1 = a |

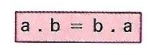
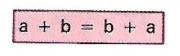

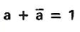
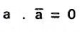
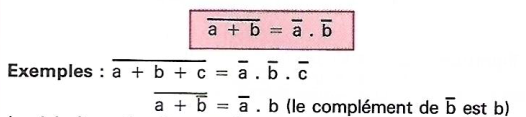
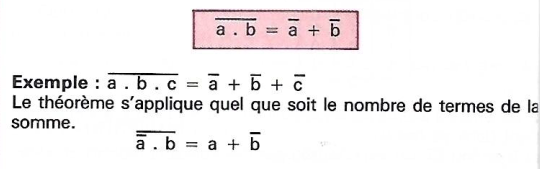
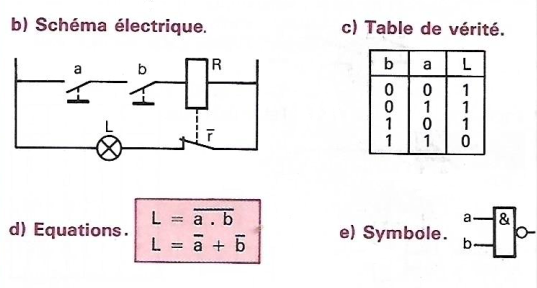
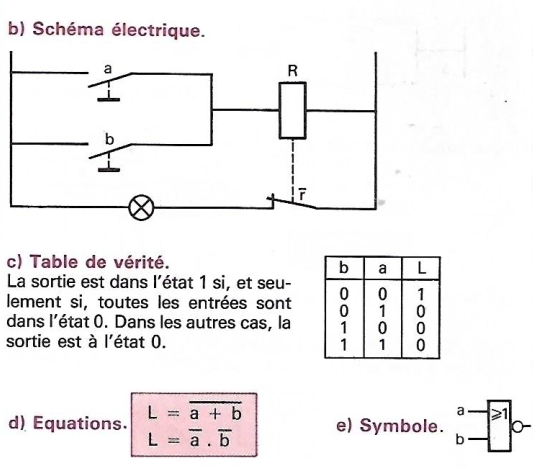
No comments to display
No comments to display