01.1 Fonctions (OUI - NON) (ET - OU)
I. La logique binaire
Avec l'évolution des automatismes, qu'ils soient électriques, pneumatiques, électroniques, on a été conduit à utiliser les méthodes d'étude de la logique binaire.
Le contact électrique permet de bien visualiser l'état passant ou l'état non passant du courant dans un circuit. Nous l'utiliserons le plus souvent pour représenter les valeurs binaires 0 et 1.
a) Contact à Fermeture |
C'est un contact qui est normalement ouvert au repos et qui se ferme lorsqu'il est actionné.On désigne ce type de contact par des lettres a , b , c , d , ... |
|
b) Contact à Ouverture |
C'est un contact qui est normalement fermé au repos et qui s'ouvre lorsqu'il est actionné.On désigne ce type de contact par des lettres surmontée d'une barre : |
|
II. Les fonctions logiques
Fonction |
OUI |
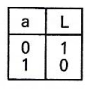
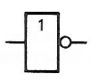
NON |
Schéma |
|
|
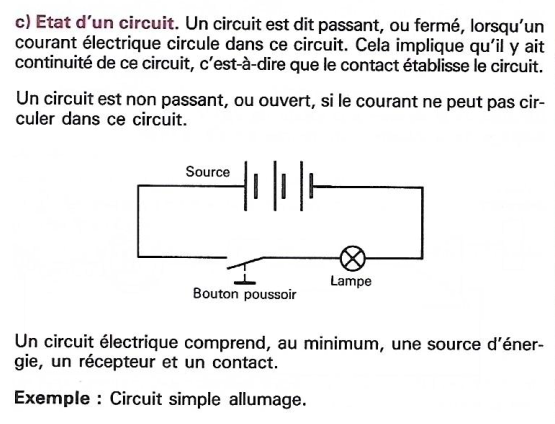
Équation |
|
|
Table de vérité |
|
|
Définition |
|
|
Symbole Logique |
 |
|
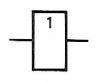Fonction |
ET (Intersection) |
Schéma |
|
Équation |
|
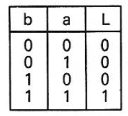
Table de Vérité |
|
Définition |
|
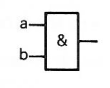
Symbole Logique |
|
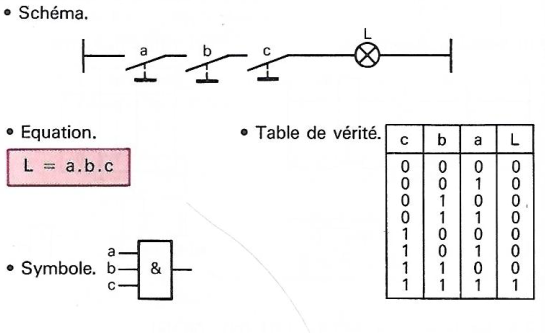
Cas de 3 Variables |
|
Fonction |
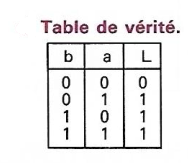
OU (Union) |
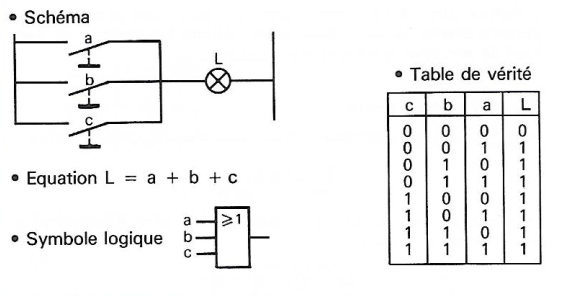
Schéma |
|
Équation |
|
Table de Vérité |
|
Définition |
|
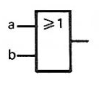
Symbole Logique |
|
| Cas de 3 Variables |
|
III. Applications
3.1 Transcrire un schéma électrique en équation logique
|
|
|
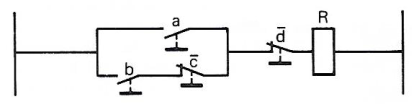
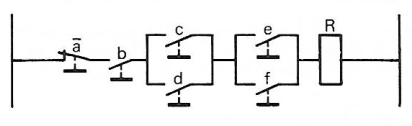
Soit le schéma d'alimentation d'une bobine de relais R à traduire en équation logique :
|
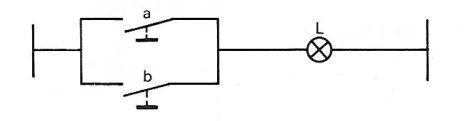
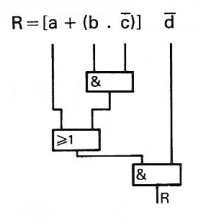
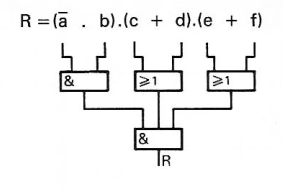
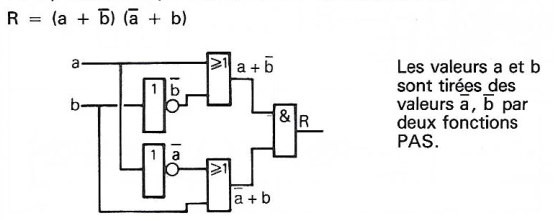
3.2 Traduire une équation en schéma électrique
|
|
|
Cela donne le schéma suivant :
|
3.3 Traduire une équation en logigramme
On représente l'équation en utilisant les symboles logiques :
|
|
|
Remarque : Les fonctions logiques ET , OU peuvent avoir 2, 3, 4, jusqu'à n entrées.
La représentation peut aussi se faire horizontalement :
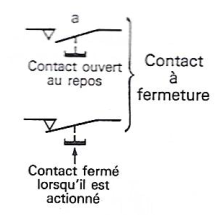
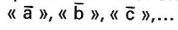
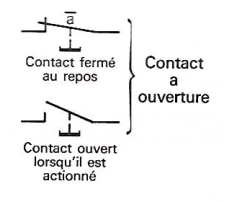
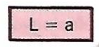
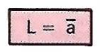
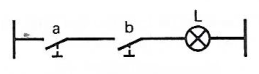
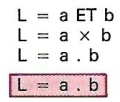
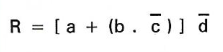
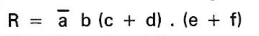
No comments to display
No comments to display